在学习数学和物理等科学领域的时候,我们经常会遇到发散和收敛的概念。这两个概念在数学和物理中都有着非常重要的应用。那么,如何判断一个数列或者一个级数是发散还是收敛呢?本文将从多个方面进行阐述。
一、数列的发散和收敛
1.1 定义
数列是由一系列有序的数所组成的序列。数列的收敛性指的是当数列的项趋向于某个数时,这个数就是数列的极限。如果数列没有极限,那么它就是发散的。
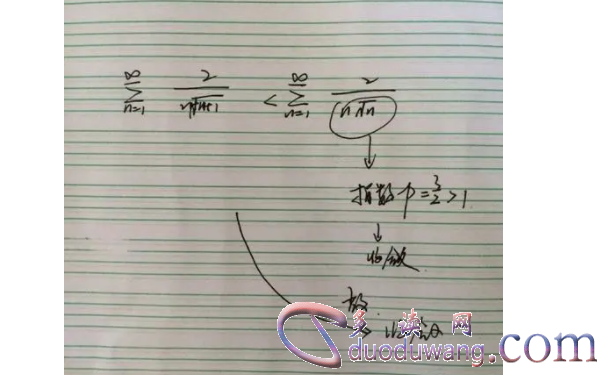
1.2 判断方法
判断一个数列是否收敛,可以通过计算它的极限来确定。如果极限存在,那么数列就是收敛的;如果极限不存在,那么数列就是发散的。
1.3 例子
例如,数列{1,2,3,4,……}的极限不存在,所以它是发散的。而数列{1,1/2,1/3,1/4,……}的极限是0,因此它是收敛的。
二、级数的发散和收敛
2.1 定义
级数是由一系列数列的和所组成的数列。级数的收敛性指的是当级数的部分和趋向于某个数时,这个数就是级数的和。如果级数的和不存在,那么它就是发散的。
2.2 判断方法
判断一个级数是否收敛,可以通过计算它的部分和来确定。如果部分和收敛于某个数,那么级数就是收敛的;如果部分和发散,那么级数就是发散的。
2.3 例子
例如,级数1+2+3+4+……的部分和无限增加,因此它是发散的。而级数1+1/2+1/3+1/4+……的部分和是有限的,因此它是收敛的。

三、函数的发散和收敛
3.1 定义
函数的收敛性指的是当自变量趋向于某个数时,函数值趋向于某个数。如果函数值没有极限,那么它就是发散的。
3.2 判断方法
判断一个函数是否收敛,可以通过计算它的极限来确定。如果极限存在,那么函数就是收敛的;如果极限不存在,那么函数就是发散的。
3.3 例子
例如,函数f(x)=1/x在x=0处的极限不存在,因此它是发散的。而函数g(x)=sin(x)/x在x=0处的极限是1,因此它是收敛的。
四、级数收敛的判别法
4.1 比较判别法
如果级数的每一项都大于等于另一个级数的对应项,而另一个级数是收敛的,那么原级数也是收敛的。
4.2 比值判别法
如果级数的项之比趋近于某个数L,那么当L<1时,级数收敛;当L>1时,级数发散;当L=1时,判别不出结果。
4.3 根值判别法
如果级数的项的绝对值开n次方趋近于某个数L,那么当L<1时,级数收敛;当L>1时,级数发散;当L=1时,判别不出结果。
本文从数列、级数、函数和级数收敛的判别法等多个方面对发散和收敛的判断方法进行了详细的阐述。通过本文的学习,相信读者们对于这个问题会有更加深入的理解和认识。
总结:谢谢大家的阅读。