在数学中,arcsinx是一种常见的反三角函数,它的原函数被称为反正弦函数。它在解决三角函数问题时起着重要的作用。本文将从多个方面对arcsinx的原函数进行详细阐述。
1、arcsinx的定义
arcsinx的定义是:对于任意实数y,如果-1≤y≤1,则arcsinx=y的唯一实数解x,其中x∈[-π/2,π/2]。这个定义表明,arcsinx的定义域是[-1,1],值域是[-π/2,π/2]。
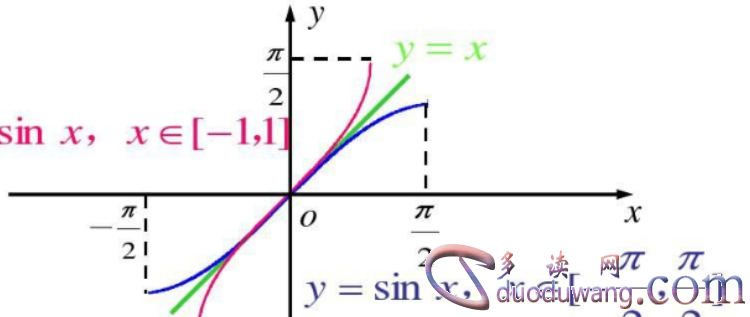
2、arcsinx的图像
arcsinx的图像是一段斜率为1的曲线,它在x=0处与y轴相交,且在x=-1和x=1处有一个垂直渐近线。这个图像对于理解arcsinx的性质非常重要。
3、arcsinx的导数
arcsinx的导数是1/√(1-x^2),这个导数可以通过求导得到。这个导数的意义是,如果我们知道了x的值,那么我们就可以求出arcsinx的斜率,也就是曲线在那个点的切线的斜率。
4、arcsinx的积分
arcsinx的积分是xarcsinx+√(1-x^2)+C,其中C是一个常数。这个积分可以通过分部积分得到。这个积分的意义是,如果我们知道了arcsinx的值,那么我们就可以求出x的值,也就是曲线在那个点的横坐标。
5、arcsinx的应用
arcsinx在三角函数问题中起着重要的作用。例如,如果我们知道sinx的值,那么我们就可以通过arcsinx求出x的值。这个应用在工程学和物理学中非常常见。
6、arcsinx的性质
arcsinx具有以下性质:
(1)arcsin(-x)=-arcsinx
(2)arcsin(x)+arcsin(-x)=0
(3)arcsin(x)=π/2-arcsin(1/x)
(4)arcsin(x)=arccos(√(1-x^2))
(5)arcsin(x)≤x≤π/2
这些性质对于理解arcsinx的性质非常重要。
7、arcsinx的应用举例
arcsinx在三角函数问题中有着广泛的应用。例如,如果我们知道sinx的值是1/2,那么我们就可以通过arcsinx求出x的值是π/6。这个应用在工程学和物理学中非常常见。
8、arcsinx的计算方法
arcsinx的计算方法可以通过泰勒级数得到。例如,arcsinx=x+x^3/6+x^5/40+...。这个计算方法可以用于计算arcsinx的近似值。
9、arcsinx的拓展
arcsinx可以拓展到复数域上,这个拓展被称为复反正弦函数。复反正弦函数在复分析中有着广泛的应用。
10、arcsinx的应用前景
arcsinx在工程学和物理学中有着广泛的应用前景。随着科技的发展,arcsinx的应用前景将会越来越广泛。
arcsinx是一种常见的反三角函数,它的原函数被称为反正弦函数。它在解决三角函数问题时起着重要的作用。本文从多个方面对arcsinx的原函数进行了详细阐述,包括定义、图像、导数、积分、应用、性质、计算方法、拓展和应用前景等方面。通过本文的阅读,读者可以更加深入地理解arcsinx的性质和应用。