在微积分中,泰勒展开式是一种常用的数学工具,用来近似一个函数在某一点附近的行为。当我们谈到sinx的泰勒展开式时,我们通常是指将sinx在某一点附近展开成无限级数的形式,以便更好地研究和理解sinx的性质。
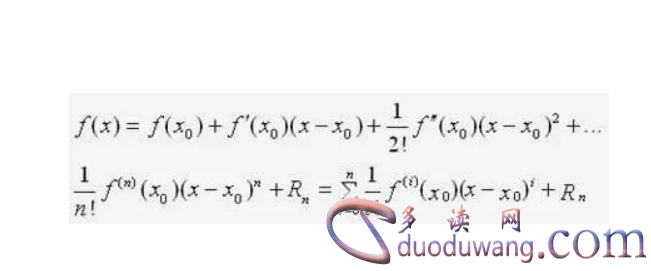
1. 泰勒展开式的定义
泰勒展开式是一种将一个函数在某一点附近展开成无限级数的方法。对于一个函数f(x),其在x=a处的泰勒展开式表示为:
f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...
2. sinx的泰勒展开式
sinx是一个基本的三角函数,其泰勒展开式在x=0处展开为:
sinx = x - x^3/3! + x^5/5! - x^7/7! + ...
3. 求解sinx的泰勒展开式
为了求解sinx在x=0处的泰勒展开式,我们需要计算sinx在x=0处的各阶导数。通过对sinx进行求导,我们可以得到:
sin(0) = 0
cos(0) = 1
-sin(0) = 0
-cos(0) = -1

4. 计算sinx的泰勒展开式
根据泰勒展开式的定义,我们可以将sinx在x=0处展开为一个无限级数:
sinx = x - x^3/3! + x^5/5! - x^7/7! + ...
5. 泰勒展开式的应用
泰勒展开式在数学、物理、工程等领域有着广泛的应用。在物理学中,泰勒展开式可以用来近似复杂函数的行为,从而简化物理模型的求解过程。在工程中,泰勒展开式可以用来优化电路设计、信号处理等问题的求解。
6. sinx的泰勒展开式的收敛性
sinx的泰勒展开式是一个无穷级数,其收敛性取决于x的取值范围。当x的取值范围在[-π, π]内时,sinx的泰勒展开式可以收敛于sinx的真实值。但是当x的取值范围超出[-π, π]时,泰勒展开式可能会出现收敛性问题。
7.
泰勒展开式是一种用来近似函数行为的重要工具,而sinx的泰勒展开式可以帮助我们更好地理解sinx的性质和行为。通过计算sinx在x=0处的泰勒展开式,我们可以将sinx表示为一个无限级数,从而更好地理解sinx在不同取值范围内的行为。
在数学和物理的研究中,泰勒展开式扮演着重要的角色,它可以帮助我们理解复杂函数的行为,并简化问题的求解过程。sinx的泰勒展开式不仅展示了sinx的性质,还让我们对三角函数的特性有了更深入的认识。希望读者通过本文的介绍,更好地理解和运用泰勒展开式以及sinx的泰勒展开式。