三角函数是高中数学学习的基础性知识,它所涉及的正弦、余弦等概念,对于我们解题也是十分重要的。而掌握三角函数的图像与性质,更可以为我们以后深入学习数学打下坚实的基础。
一、正弦函数的性质
我们来了解正弦函数的图像与性质。
正弦函数y=Asin(ωx+φ)+b的图像如下所示:
1. 周期性:正弦曲线的周期为2π/ω,ω为正弦曲线函数最小正周期,而一个摆动的周期正好是一个完整的正弦曲线的周期。
2. 对称性:正弦曲线对于x轴中点对称,即若τ是正弦函数的周期,则sin(τ-x)=sin(x)
3. 奇偶性:正弦曲线为奇函数,即 sin(?x)=?sin(x) 。
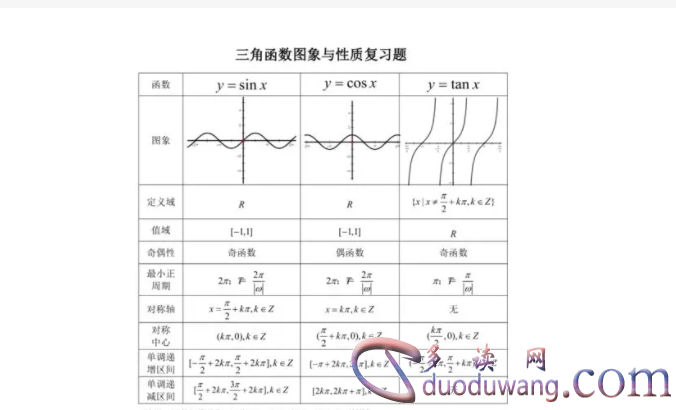
二、余弦函数的性质
接下来我们来了解余弦函数的性质。
余弦函数y=Acos(ωx+φ)+b的图像如下所示:
1. 周期性:余弦曲线的周期为2π/ω, 与正弦曲线一样。
2. 对称性:余弦曲线对于y轴中点对称,即cos(-x)=cos(x)
3. 奇偶性:余弦曲线为偶函数,即cos(?x)=cos(x)。
三、正切函数的性质
最后我们来了解正切函数的性质。
正切函数y=A tan(ωx+φ)+b的图像如下所示:
1. 周期性:正切曲线的周期为π/ω,π/ω为T即最小正周期右侧的区间长度为T/2。
2. 对称性:正切曲线对于x轴中点不对称,但对于原点的对称。
3. 奇偶性:正切曲线为奇函数,即tan(-x)=(-tan(x))。
经过上述的介绍,我们已经了解了三角函数的图像与性质。掌握这些性质,我们可以更好的理解三角函数,并且将其运用到实际问题中去,在解决问题的时候准确无误地制定出方案,从而提高自己的数学水平。