三角函数是初中数学中的重要知识点,也是高中数学和大学数学中不可避免地会涉及到的内容。在三角函数中,基本公式是非常重要的基础。本篇文章将会为大家详细介绍三角函数基本公式,希望对大家的学习有所帮助。
一、正弦函数、余弦函数和正切函数的基本公式
在三角函数中,最基础的三个函数是正弦函数(sin)、余弦函数(cos)和正切函数(tan)。它们的基本公式如下:
sin(x+y) = sinx*cosy + cosx*siny
cos(x+y) = cosx*cosy - sinx*siny
tan(x+y) = (tanx + tany)/(1 - tanx*tany)
这三个公式我们需要特别记忆,因为它们是解决三角函数问题时最经常用到的。当然,在应用这些公式之前,我们还需要掌握一些基本的三角函数性质和公式。
二、三角函数的基本性质和公式
在三角函数中,有一些基本的性质和公式是我们必须掌握的。这些性质和公式是使用三角函数的前提条件,也是我们使用三角函数解题的基础。
1. 三角函数的定义域和值域
三角函数中,正弦函数和余弦函数的定义域是实数集R,其值域是[-1,1];而正切函数的定义域是{x∣x∈R,x≠(2k+1)π/2},其值域是(-∞,∞)。
2. 三角函数的周期性
正弦函数和余弦函数的周期是2π,正切函数的周期是π。
3. 三角函数的对称性
正弦函数和余弦函数是偶函数,即sin(-x) = -sinx,cos(-x) = cosx;而正切函数是奇函数,即tan(-x) = -tanx。
4. 三角函数的反函数
正弦函数、余弦函数和正切函数都有反函数,并且它们的反函数分别是反正弦函数、反余弦函数和反正切函数。它们的定义域都是[-1,1],值域依次是[-π/2,π/2]、[0,π]和(-π/2,π/2)。
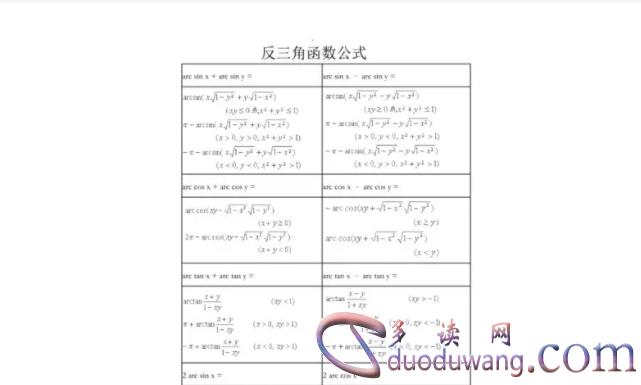
除此之外,还有很多三角函数的性质和公式,比如三角函数的和差化积公式、倍角公式、半角公式等等。这些公式虽然不如基本公式那么重要,但在高中或大学的数学学习中也非常重要。
三、三角函数的应用
三角函数的应用非常广泛,例如在物理、工程、天文、经济等方面都会使用到。其中,最常见的应用莫过于三角函数解题了。
在解题时,我们需要结合相应的知识点,运用所学的三角函数性质和公式,来确定解题的路线和方法。具体来说,我们可以通过以下几个步骤来解决三角函数问题:
1. 确定问题中的三角函数类型,例如是正弦函数还是余弦函数等。
2. 掌握题目所给的信息,明确目标,确定解题方法。
3. 运用三角函数的公式和性质进行化简和计算。
4. 验证结果,保留正确位数。
结语:
三角函数的基本公式是解决三角函数问题的基础,同时三角函数的性质和公式也是我们使用三角函数的前提条件。通过掌握这些知识,我们能够更好地理解三角函数,从而更轻松地解决问题。希望本篇文章对大家的学习有所帮助。