在数学中,奇变偶不变符号是一个非常重要的概念,它可以帮助我们更好地理解象限。那么,奇变偶不变符号看象限怎么理解呢?本文将从多个方面进行阐述。
1、奇变偶不变符号的定义
奇变偶不变符号是一个数学符号,用于描述函数在坐标系中的对称性。如果一个函数是奇函数,那么它在原点处对称;如果一个函数是偶函数,那么它在y轴上对称。
2、奇变偶不变符号与象限的关系
在二维坐标系中,我们可以将坐标轴分为四个象限。当我们考虑一个函数在象限中的对称性时,奇变偶不变符号就非常有用了。具体来说,如果一个函数是奇函数,那么它在第一象限和第三象限中对称;如果一个函数是偶函数,那么它在第二象限和第四象限中对称。
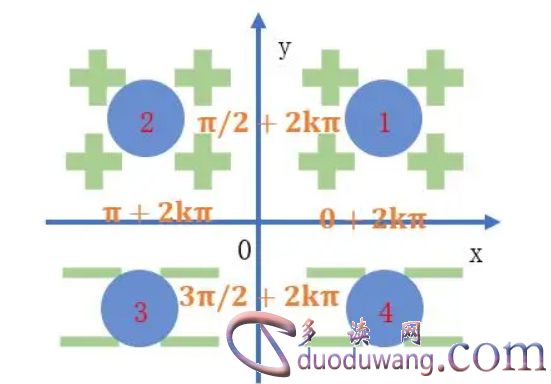
3、奇变偶不变符号的应用
奇变偶不变符号在数学中有着广泛的应用。例如,在求解积分时,我们可以利用奇变偶不变符号来简化计算。如果被积函数是奇函数,那么积分结果为0;如果被积函数是偶函数,那么积分结果可以通过对称性简化计算。
4、奇变偶不变符号的意义
奇变偶不变符号的意义在于帮助我们更好地理解函数的对称性。通过观察函数的奇偶性,我们可以得到很多有用的信息,例如函数的零点、最值等。奇变偶不变符号还可以帮助我们更好地理解函数的图像。

5、奇变偶不变符号的推导
奇变偶不变符号的推导是一个比较复杂的过程,需要运用到一些高级的数学知识。在这里,我们简单介绍一下奇变偶不变符号的推导方法。我们将函数表示为一个泰勒级数,然后观察泰勒级数中各项的系数。如果泰勒级数中奇数次项的系数都为0,那么函数是偶函数;如果泰勒级数中偶数次项的系数都为0,那么函数是奇函数。
6、奇变偶不变符号的实例
我们来看一个奇变偶不变符号的实例。考虑函数f(x)=x^3,我们可以通过求导得到它的导函数f'(x)=3x^2。观察导函数的奇偶性,我们可以发现它是一个奇函数。原函数f(x)是一个偶函数,它在第二象限和第四象限中对称。
通过以上多个方面的阐述,我们可以更好地理解奇变偶不变符号对象限的意义。奇变偶不变符号不仅可以帮助我们简化计算,还可以帮助我们更好地理解函数的对称性。在数学学习中,我们应该充分利用奇变偶不变符号这个工具,加深对函数的理解。
总结:数学是一门非常有趣的学科,希望大家在学习中能够享受到其中的乐趣。