奇变偶不变符号看象限是什么意思?这是一道高中数学中的常见问题。奇变偶不变符号是数学中的一个重要概念,它可以用来判断一个函数在不同象限中的正负性,进而帮助我们解决数学问题。本文将从多个方面对奇变偶不变符号看象限是什么意思做详细的阐述。
1、奇变偶不变符号的定义
奇变偶不变符号是指一个函数在不同象限中的正负性是否相同。奇函数是指在某一象限内,当自变量取相反数时,函数值也取相反数;偶函数是指在某一象限内,当自变量取相反数时,函数值不变。符号函数是指当自变量大于0时,函数值为1;当自变量小于0时,函数值为-1。
2、奇变偶不变符号的应用
奇变偶不变符号可以用来判断一个函数在不同象限中的正负性。当一个函数在某一个象限中为正数时,在相对的象限中也为正数,而在相对的象限中为负数。这个性质可以用来解决一些数学问题,如求解方程、不等式等。
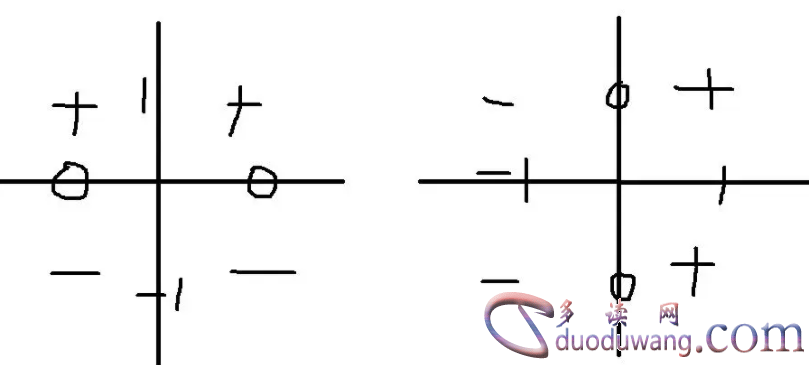
3、奇变偶不变符号的例子
例如,函数f(x) = x^3是一个奇函数,因为当x取相反数时,f(x)也取相反数。函数g(x) = x^2是一个偶函数,因为当x取相反数时,g(x)不变。符号函数h(x) = sign(x)是一个奇函数,因为当x取相反数时,h(x)也取相反数。
4、奇变偶不变符号的推导
奇变偶不变符号可以通过对函数进行推导得到。例如,对于一个函数f(x),如果f(-x) = -f(x),那么f(x)就是一个奇函数;如果f(-x) = f(x),那么f(x)就是一个偶函数。符号函数也可以通过这种方式来推导。
5、奇变偶不变符号的应用举例
奇变偶不变符号在数学中有很多应用。例如,在解决一些不等式问题时,我们可以利用奇变偶不变符号来判断不等式的解集。又如,在求解一些积分问题时,我们可以利用奇变偶不变符号来简化计算。

6、奇变偶不变符号的局限性
奇变偶不变符号虽然在数学中有很多应用,但它也有一定的局限性。例如,对于一些复杂的函数,它可能无法判断其奇偶性。对于一些非函数的表达式,奇变偶不变符号也无法应用。
7、奇变偶不变符号的发展
随着数学的发展,奇变偶不变符号也在不断地发展。例如,人们发现了一些新的奇偶性质,如半奇函数、半偶函数、周期函数等。这些新的奇偶性质为我们解决一些更为复杂的数学问题提供了更多的工具。
奇变偶不变符号是数学中的一个重要概念,它可以用来判断一个函数在不同象限中的正负性,进而帮助我们解决数学问题。本文从奇变偶不变符号的定义、应用、例子、推导、应用举例、局限性和发展等多个方面进行了详细的阐述。奇变偶不变符号虽然有一定的局限性,但随着数学的发展,它也在不断地发展。